OKID(Observer Kalman Filter Identification)는 시간 영역에서 비선형 시스템의 입출력 데이터로부터 이산시간 선형 상태 공간 모델을 식별하는 알고리즘입니다.
OKID는 1990년대 초 NASA의 Juang이 개발한 이후 많은 항공기와 우주선의 모델을 식별하기 위해 도입되었습니다.
ERA(Eigensystem Realization Algorithm)의 확장으로서 OKID는 ERA 알고리즘의 두 가지 근본적인 한계를 해결합니다.
제약 조건은 시스템의 초기 값이 \(0\)이어야 하고 시스템이 안정적이어야 한다는 것입니다. 이러한 한계로 인해 실제 알고리즘 적용에 어려움이 있는데, 예를 들어 실제 환경에서는 돌풍, 난기류와 같은 작은 대기 교란이 있어도 일반적으로 항공기의 트림 상태는 불완전하므로 시스템의 초기값 \(0\)은 작동하지 않으며, 시스템의 안정성이 낮을 경우 정상 상태에 도달하는 데 상당한 시간이 걸리므로 과도한 입/출력 데이터를 저장하고 처리해야 합니다.
시스템의 안정성을 인위적으로 높일 수 있는 방법이 있습니까? 안정성이 높거나 감쇠가 빠르면 시스템 응답에 대한 초기 값의 영향이 크게 줄어들고 입력 및 출력 데이터의 양이 줄어들어 ERA 문제를 해결할 수 있습니다. 이것은 피드백 컨트롤러를 설계하는 문제와 같습니다. OKID는 프로세스를 사용하여 다음과 같은 동일한 효과를 얻습니다. 나. 아래와 같이 대수적 조작을 통한 피드백 제어기를 추가하여 안정성을 높인다.
미지의 비선형 시스템을 어떤 평형점에서 선형화하여 얻은 모델이 수학식 1과 같이 이산시간 선형 시스템으로 표현된다고 가정하자.
\( \begin{정렬} & \mathbf{x}_{k+1}=A \mathbf{x}_k+B \mathbf{u}_k \tag{1} \\ \\ & \mathbf{y} _k=C \mathbf{x}_k+D \mathbf{u}_k \end{align} \)
여기서 \(\mathbf{x}_k \in \mathbb{R}^n\), \(\mathbf{u}_k \in \mathbb{R}^p\), \(\mathbf{y}_k \ \mathbb{R}^{q\), \(A \in \mathbb{R}^{n \times n}\), \(B \in \mathbb{R}^{n \times p}\ ) , \(C\in \mathbb{R}^{q\times n}\) 및 \(D\in \mathbb{R}^{q\times p}\).
수학식 1의 상태 업데이트 항에 \(G \mathbf{y}_k\)를 더하고 빼도 방정식은 변하지 않지만 다음과 같이 출력 피드백 형태로 변환할 수 있습니다. 이것이 OKID의 핵심 아이디어입니다.
\( \begin{정렬} \mathbf{x}_{k+1} &= A \mathbf{x}_k+B \mathbf{u}_k+G \mathbf{y}_k-G \mathbf{y} _k \tag{2} \\ \\ &=(A+GC) \mathbf{x}_k+(B+GD) \mathbf{u}_k-G \mathbf{y}_k \\ \\ &= \tilde {A} \mathbf{x}_k+ \tilde{B} \mathbf{v}_k \end{align} \)
여기서 \(G\in \mathbb{R}^{n\times q}\)는 관찰자 이득이라고 합니다.
\( \begin{align} & \tilde{A}=A+GC \ \ \in \mathbb{R}^{n \times n} \tag{3} \\ \\ & \tilde{B}= ( B+GD \ \ -G) \ \ \in \mathbb{R}^{n \times (p+q)} \\ \\ & \mathbf{v}_k= \begin{bmatrix} \mathbf{u} _k \\ \mathbf{y}_k \end{bmatrix} \ \ \in \mathbb{R}^{(p+q)} \end{align} \)
오전. 관찰자 이득 \(G\)는 안정적인 것으로 \(\tilde{A}\)를 선택합니다. 방정식 (1)과 (2)는 수학적으로 동일합니다.
이제 방정식 (2)의 상태 업데이트 방정식을 시간 단계 \(k=i\)에서 \(k=i+l_0\)로 확장해 보겠습니다.
\( \begin{정렬} \mathbf{x}_{i+1} & = \tilde{A} \mathbf{x}_i+ \tilde{B} \mathbf{v}_i \tag{4} \\ \ \ \mathbf{x}_{i+2} & = \tilde{A} \mathbf{x}_{i+1}+ \tilde{B} \mathbf{v}_{i+1} \\ & = \tilde{A}^2 \mathbf{x}_i+ \tilde{A} \tilde{B} \mathbf{v}_i+ \tilde{B} \mathbf{v}_{i+1} \\ \\ & \ \ \ \cdots \\ \\ \mathbf{x}_{i+l_0 } &= \tilde{A} \mathbf{x}_{i+l_0-1}+ \tilde{B} \mathbf{ v}_{i+l_0-1} \\ &= \tilde{A}^{l_0 } \mathbf{x}_i+ \tilde{A}^{l_0-1} \tilde{B} \mathbf{v} _i+ \tilde{A}^{l_0-2} \tilde{B} \mathbf{v}_{i+1}+ \cdots + \tilde{B} \mathbf{v}_{i+l_0-1} \끝{정렬} \)
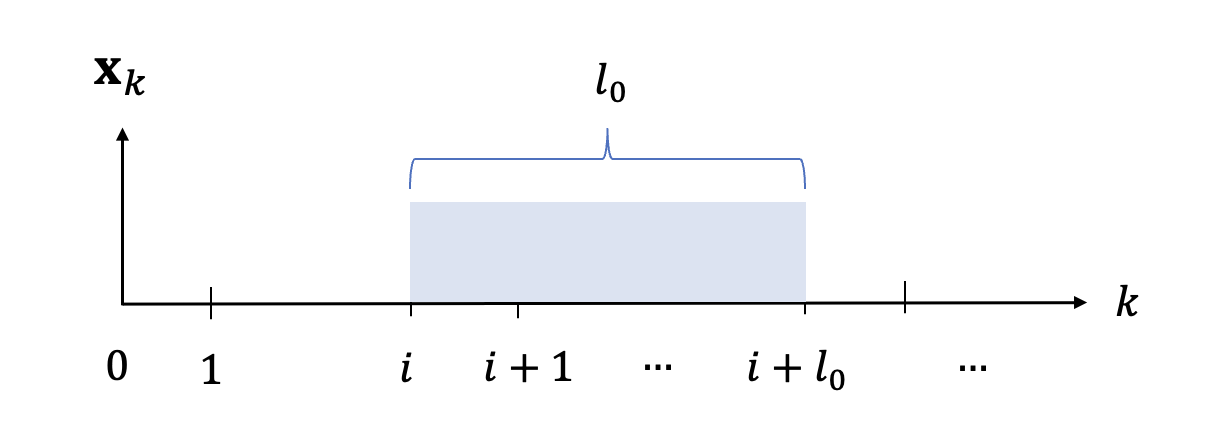
수학식 1의 측정식은 수학식 4에 의해 시간 스텝 \(k=i+l_0\)에서 다음과 같이 된다.
\( \begin{정렬} \mathbf{y}_{i+l_0 } &= C \mathbf{x}_{i+l_0 }+D \mathbf{u}_{i+l_0 } \tag{5} \\ \\ &=C \tilde{A}^{l_0 } \mathbf{x}_i+C \tilde{A}^{l_0-1} \tilde{B} \mathbf{v}_i+C \tilde {A}^{l_0-2} \tilde{B} \mathbf{v}_{i+1} \\ & \ \ \ \ + \cdots + C \tilde{B} \mathbf{v}_{i +l_0-1}+D \mathbf{u}_{i+l_0 } \end{align} \)
이제 방정식 (5)를 \(i=0, 1, \cdots, l-1\) 또는 시간 단계 \(k=l_0, l_0+1, \cdots, l_0+l-1\)에서 풀면 동등한 방법을 얻으십시오
\( \begin{정렬} \mathbf{y}_{l_0 } &= C \tilde{A}^{l_0 } \mathbf{x}_0+ C \tilde{A}^{l_0-1} \tilde{B } \mathbf{v}_0+C \tilde{A}^{l_0-2} \tilde{B} \mathbf{v}_1 \tag{6} \\ & \ \ \ \ \ + \cdots + C\ 물결표{B} \mathbf{v}_{l_0-1}+D \mathbf{u}_{l_0 } \\ \\ \mathbf{y}_{l_0+1} &=C \tilde{A}^ {l_0 } \mathbf{x}_1+C \tilde{A}^{l_0-1} \tilde{B} \mathbf{v}_1+C \tilde{A}^{l_0-2} \tilde{B } \mathbf{v}_2 \\ & \ \ \ \ \ + \cdots + C\tilde{B} \mathbf{v}_{l_0 }+D \mathbf{u}_{l_0+1} \\ \ \ \mathbf{y}_{l_0+2} &=C \tilde{A}^{l_0 } \mathbf{x}_2+C \tilde{A}^{l_0-1} \tilde{B} \mathbf {v}_2+C \tilde{A}^{l_0-2} \tilde{B} \mathbf{v}_3 \\ & \ \ \ \ \ + \cdots + C \tilde{B} \mathbf{v }_{l_0+1}+D \mathbf{u}_{l_0+2} \\ \\ & \ \ \ \cdots \\ \\ \mathbf{y}_{l_0+l-1} &=C \tilde{A}^{l_0 } \mathbf{x}_{l-1}+C \tilde{A}^{l_0-1} \tilde{B} \mathbf{v}_{l-1}+ C \tilde{A}^{l_0-2} \tilde{B}\mathbf{v}_l \\ & \ \ \ \ \ + \cdots + C \tilde{B} \mathbf{v}_{l_0+ l -2}+D \mathbf{u}_{l_0+l-1} \end{align} \)
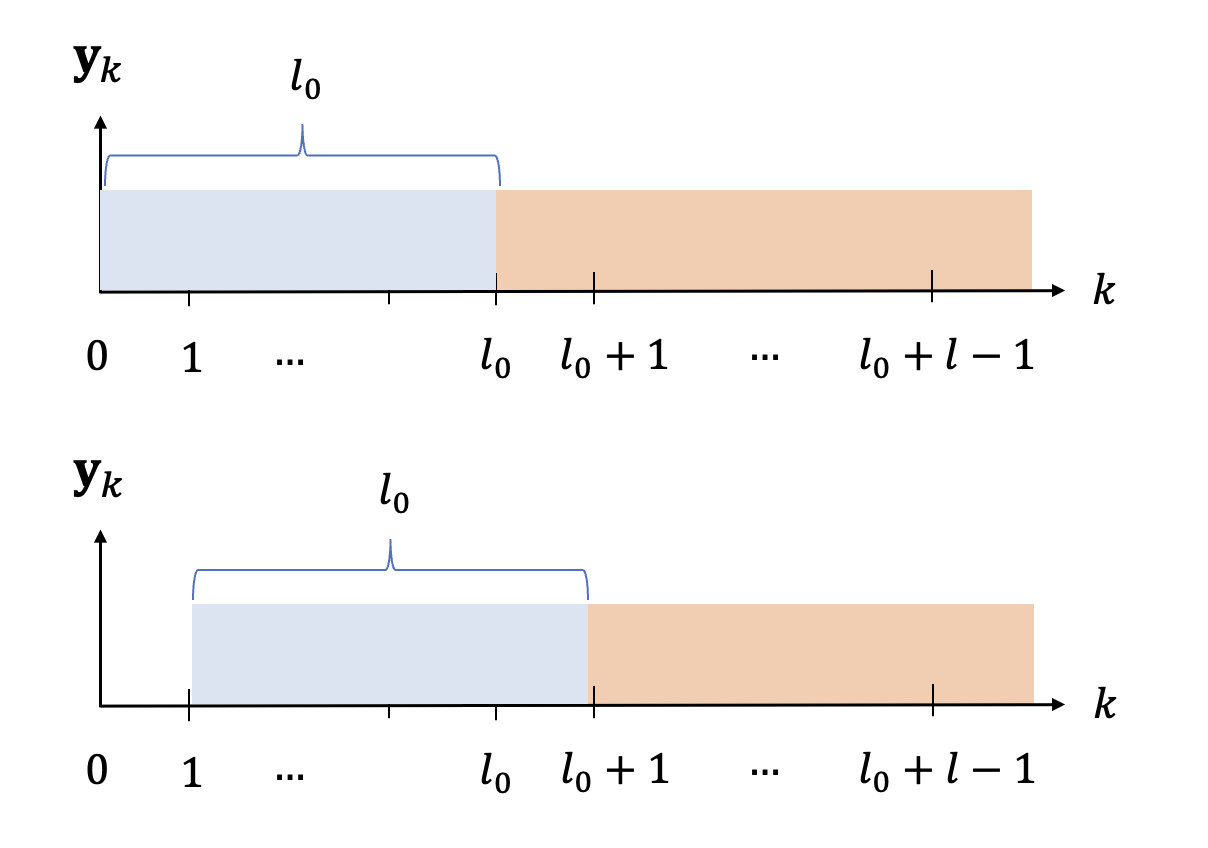
수학식 6은 다음과 같이 행렬 형태로 정리할 수 있다.
\( \mathbf{y}_{l_0:l_0+l-1}=C \tilde{A}^{l_0 } \mathbf{x}_{0:l-1}+ \bar{Y}V \tag {7}\)
여기
\( \begin{정렬} & \mathbf{y}_{l_0:l_0+l-1}=( \mathbf{y}_{l_0} \ \ \ \mathbf{y}_{l_0+1} \ \ \ \mathbf{y}_{l_0+2} \ \ \ \cdots \ \ \ \mathbf{y}_{l_0+l-1} ) \ \ \in \mathbb{R}^{q \times l} \tag{8} \\ \\ & \mathbf{x}_{0:l-1} =( \mathbf{x}_0 \ \ \ \mathbf{x}_1 \ \ \ \mathbf{x}_2 \ \ \ \cdots \ \ \ \mathbf{x}_{l-1} ) \ \ \in \mathbb{R}^{n \times l} \\ \\ & \bar{Y} = (D \ \ \ C \tilde{B} \ \ \ C\tilde{A}\tilde{B} \ \ \ \cdots \ \ \ C\tilde{A}^{l_0-2} \tilde{B} \ \ \ C \tilde{A}^{l_0-1} \tilde{B} ) \ \ \in \mathbb{R}^{q \times ((p+q) l_0+p)} \\ \\ & V= \ 시작{bmatrix} \mathbf{u}_{l_0 } & \mathbf{u}_{l_0+1} & \mathbf{u}_{l_0+2} & \cdots & \mathbf{u}_{l_0+ l -1} \\ \mathbf{v}_{l_0-1} & \mathbf{v}_{l_0 } & \mathbf{v}_{l_0+1} & \cdots & \mathbf{v}_{ l_0 +l-2} \\ \vdots & \cdots & \vdots & \ddots & \vdots \\ \mathbf{v}_1 & \mathbf{v}_2 & \mathbf{v}_3 & \cdots & \mathbf { v}_l \\ \mathbf{v}_0 & \mathbf{v}_1 & \mathbf{v}_2 & \cdots & \mathbf{v}_{l-1} \end{bmatrix} \ \ \mathbb { R}^{((p+q) l_0+p) \t 임스 l} \e nd{정렬} \)
오전. \(\bar{Y}\)는 관찰자 Markov 매개변수의 행렬입니다.
\(l_0\)이 여기서 충분히 크게 설정되어 \(\tilde{A}^{l_0 } \approx 0\)이면 식 (7)은 다음과 같이 됩니다.
\( \mathbf{y}_{l_0:l_0+l-1} \approx \bar{Y}V \tag{9} \)
\( \mathbf{y}_{l_0:l_0+l-1}\) 및 \(V\)는 입력 데이터와 출력 데이터로만 구성된 행렬이며 Markov 매개 변수 행렬 \(\bar{Y}\ )는 추정할 시스템을 형성하는 행렬
방정식 (9)에 따르면 초기 값의 영향이 사라집니다. 또한, 수학식 9에 따르면 방정식의 총 수는 \(q \times l\)이고 추정할 미지수의 수는 \(q \times ((p+q) l_0+p)\)이다. . 따라서 데이터 \(l\)의 길이가 \((p+q) l_0+p\)보다 크게 설정되면, 즉 \(l \ge (p+q) l_0+p\)이면 숫자 식의 미지의 수. 이므로 행렬 \(\bar{Y}\)는 대략 다음과 같이 계산할 수 있습니다.
\(\begin{정렬} \bar{Y} &= \mathbf{y}_{l_0:l_0+l-1} V^+ \tag{10} \\ \\ &= \mathbf{y}_{ l_0:l_0+l-1} V^T (VV^T )^{-1} \end{정렬} \)
여기서 \(V^+\)는 \(V\)의 의사 역행렬입니다. 행렬 \(V\)의 의사 역행렬이 존재하려면 시스템에 대한 입력이 모든 동작 모드를 자극할 만큼 충분히 복잡해야 합니다.
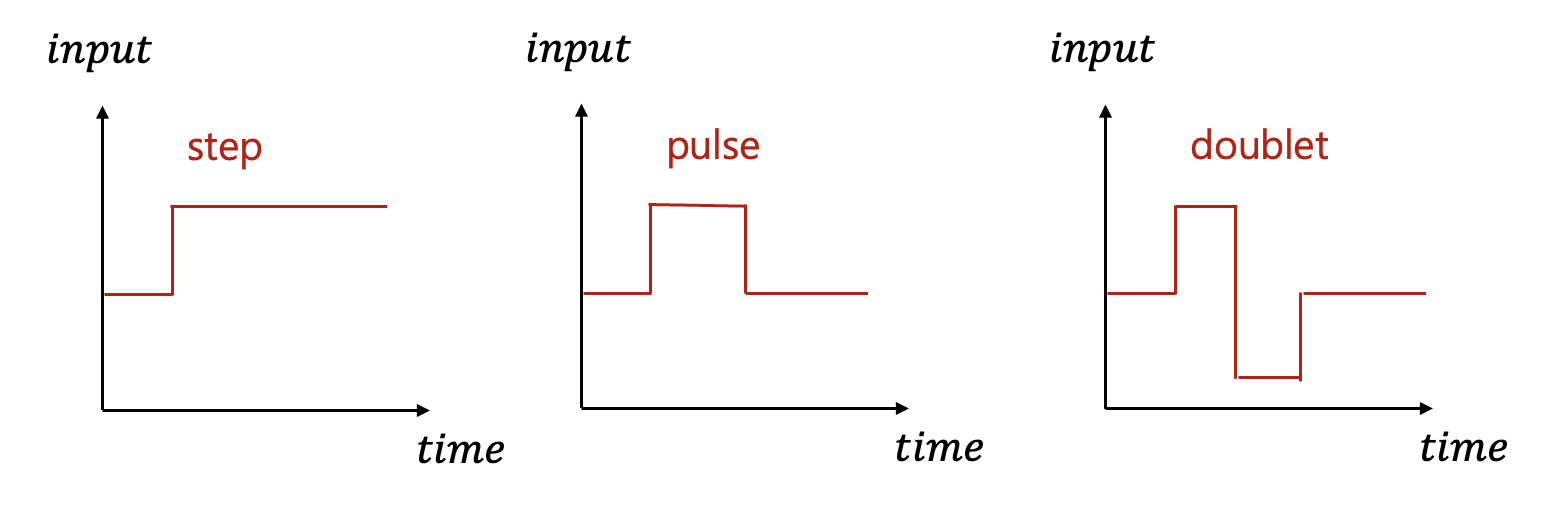
참고로 항공기 식별 비행 테스트에는 세 가지 유형의 제어 입력이 일반적으로 사용됩니다: 스텝, 임펄스, 싱글렛 및 더블렛.
이제 수학식 8을 참조하여 Markov 매개변수 행렬 \(\bar{Y}\)를 다음과 같이 나눕니다.
\(\begin{align} \bar{Y} &= (D \ \ \ C\tilde{B} \ \ \ C\tilde{A}\tilde{B} \ \ \ \cdots \ \ \ C\tilde {A}^{l_0-2} \tilde{B} \ \ \ C\tilde{A}^{l_0-1} \tilde{B} ) \tag{11} \\ \\ &= ( \bar{ Y}_0 \ \ \ \bar{Y}_1 \ \ \ \bar{Y}_2 \ \ \ \cdots \ \ \ \bar{Y}_{l_0-1} \ \ \ \bar{Y}_{ l_0 } ) \end{정렬} \)
여기서 식 (3)을 이용하여 Y ̅의 성분을 다음과 같이 쓸 수 있다.
\(\begin{정렬} \bar{Y}_0 &= D \tag{12} \\ \\ \bar{Y}_i &=C \tilde{A}^{i-1} \tilde{B} \\ \\ &=( C(A+GC)^{i-1} (B+GD) \ \ \ \ -C(A+GC)^{i-1} G) \\ \\ &=( \tilde{\bar{Y}}_i^{(1) } \ \ \ \ -\tilde{\bar{Y}}_i^{(2) } ) \end{align} \)
그러면 식 (12)로부터 원래 시스템의 Markov 매개변수를 다음과 같이 계산할 수 있습니다.
\(\begin{align} Y_1 &= CB=C(B+GD)-CGD \tag{13} \\ &= \tilde{\bar{Y}}_1^{(1) }- \tilde{\ bar{Y}}_1^{(2) } D \\ \\ Y_2 &= CAB=C(A+GC)(B+GD)-CGCB-C(A+GC)GD \\ &= \tilde{ \bar{Y}}_2^{(1) }- \tilde{\bar{Y}}_1^{(2) } Y_1- \tilde{\bar{Y}}_2^{(2) } D \ 끝{정렬} \)
방정식 (13)을 통해 모든 원래 시스템의 Markov 매개변수를 계산할 수 있습니다.
\(\begin{align} Y_0 &= D= \bar{Y}_0 \tag{14} \\ \\ Y_i & =CA^{i-1} B \\ \\ &=\tilde{\bar{ Y}}_i^{(1) }- \sum_{k=1}^{l_0} \tilde{\bar{Y}}_k^{(2)} Y_{ik} \end{align} \)
방정식 (14)에서 계산된 Markov 매개변수를 Ho-Kalman 식별 알고리즘에 대입하면 미지 시스템(1)의 행렬 \(A,B,C,D\)와 시스템 차수를 식별할 수 있습니다. 이 식별 방법은 OKID(Observer Kalman Filter Identification)로 알려져 있습니다.
OKID의 장점은 적절한 옵저버 게인 \(G\)를 선택하여 시스템 안정성을 높임으로써 감쇠가 낮은 시스템에서도 Markov 매개변수의 수를 줄일 수 있고 더 작은 Hankel 행렬을 사용하여 더 쉽게 계산할 수 있다는 것입니다.